Introduction to Mathematica

Posted by Eric Mascot on September 5, 2016

Next in super useful tools for physicists is Mathematica. If you're a physicist, I'm sure you've fiddled around a bit with Mathematica. I'll do a little intro and show how I usually utilize Mathematica.

Intro

First things first, let's do some arithmetic. You can type the same way you would a normal calculator and hit shift+enter.

intro-to-mathematica_1.png

intro-to-mathematica_2.png

Mathematica is cool and allows you to type the way you would write on paper.
We don't need the * to multiply because it can be inferred.
You can type the symbol pi by hitting esc, p, esc.
The escape key lets you type in symbols which you can find here.
You can also write exponents, square roots, and fractions using ctrl.
ctrl + 6 will type exponents intro-to-mathematica_3.png
ctrl + 2 will do a square root intro-to-mathematica_4.png
ctrl + /will make a fraction intro-to-mathematica_5.png
Rewriting the first calculation

intro-to-mathematica_6.png

intro-to-mathematica_7.png

Much more pretty.

Variables and Functions

You can use variables to do symbolic calculations. You can also assign values to variables.

intro-to-mathematica_8.png

intro-to-mathematica_9.png

Here, I use // as an after thought to apply the function Simplify

intro-to-mathematica_10.gif

intro-to-mathematica_11.png

intro-to-mathematica_12.png

You'll notice that assigned variables are black and unassigned variables are blue.
You can also assign variables as an after thought.

intro-to-mathematica_13.png

intro-to-mathematica_14.png

You may have noticed that I use the cosine function with square brackets. Square brackets are used for function parameters so avoid square brackets unless it is for functions.
We can define our own function with this notation.

intro-to-mathematica_15.png

:= is notation for delayed definition (evaluate each time the function is called).
We can now use the function.

intro-to-mathematica_16.png

intro-to-mathematica_17.png

Visualization

Let's try to visualize the function we just defined. There are many different ways to plot.

intro-to-mathematica_18.gif

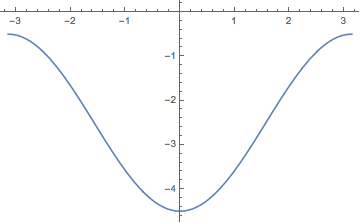
intro-to-mathematica_19.gif

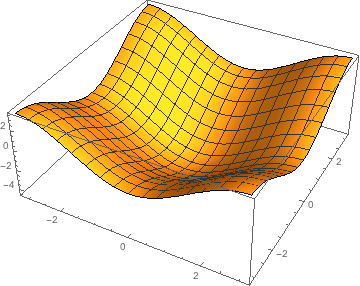
intro-to-mathematica_20.gif

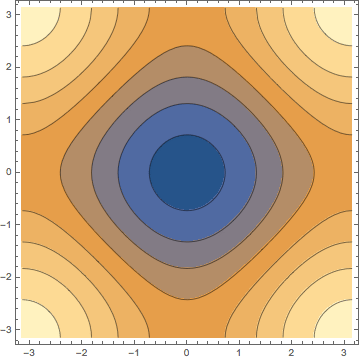
intro-to-mathematica_21.gif

You can find more ways to visualize here. You can also add options to make the plot look how you want.

intro-to-mathematica_22.png

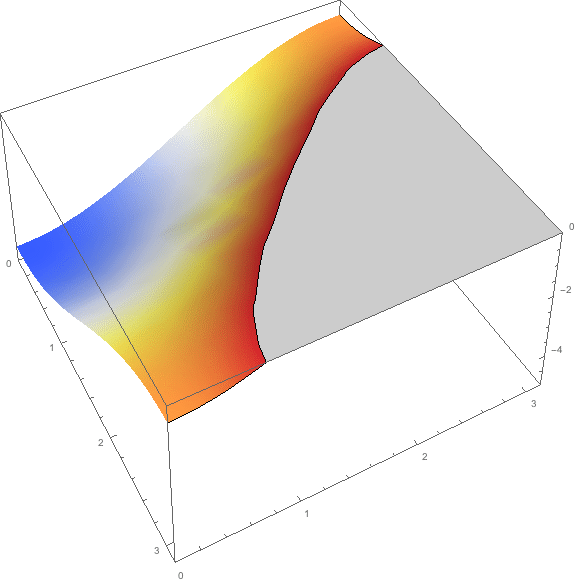
intro-to-mathematica_23.gif

You can find these options by going to the documentation. Do this by pressing F1 with the cursor on the function.

Manipulation

Here is the fun part of Mathematica. It is super easy to make interactive plots.

intro-to-mathematica_24.gif

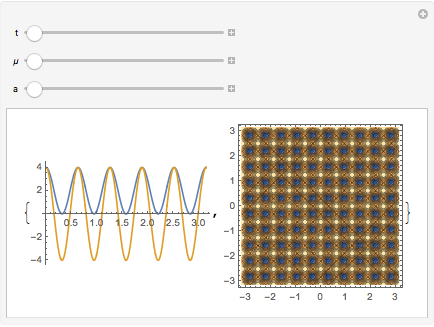
intro-to-mathematica_69.png

That is basically it. My main use of Mathematica is to visualize functions. If you want to learn more, you can move on but as long as you can plot functions, that's all you really need.

Lists

Another common need is lists which will also be used for arrays, vectors, matrices, network graphs, etc.

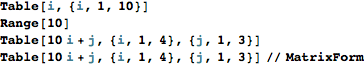
intro-to-mathematica_26.gif

intro-to-mathematica_27.png

intro-to-mathematica_28.png

intro-to-mathematica_29.png

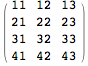
intro-to-mathematica_30.png

Access elements in a table with double square brackets

intro-to-mathematica_31.gif

intro-to-mathematica_32.png

intro-to-mathematica_33.png

If you have multiple cores, you can construct tables in parallel

intro-to-mathematica_34.gif

intro-to-mathematica_35.png

intro-to-mathematica_36.png

Map and Apply

List operations are made easier with map and apply. Map does element wise operation whereas apply does a collective operation.

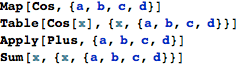
intro-to-mathematica_37.gif

intro-to-mathematica_38.png

intro-to-mathematica_39.png

intro-to-mathematica_40.png

intro-to-mathematica_41.png

Map and apply are so ubiquitous, it has its own notation.

intro-to-mathematica_42.gif

intro-to-mathematica_43.png

intro-to-mathematica_44.png

intro-to-mathematica_45.png

intro-to-mathematica_46.png

Vectors and Matrices

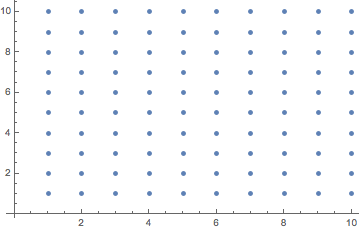
A 2D vector is just a 2 element list. Here, I make a list of coordinates.

intro-to-mathematica_47.png

intro-to-mathematica_48.png

intro-to-mathematica_49.png

intro-to-mathematica_50.gif

I can now do a matrix operation on each coordinate

intro-to-mathematica_51.gif

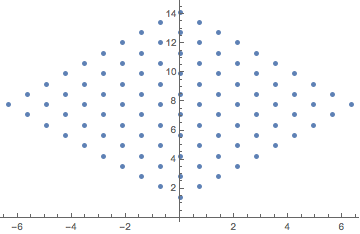
intro-to-mathematica_52.gif

To review, I defined a function that takes a point. The function rotates the point 45 degrees around the origin. I then map it onto my list of points.

Pure functions

I can do the previous operation in one line with a pure function.

intro-to-mathematica_53.png

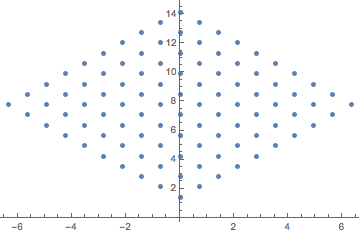
intro-to-mathematica_54.gif

This is getting a little abstract and I personally don't like all this complicated syntax but you may encounter this in other people's Mathematica notebooks. Using # and & is like an anonymous function. # means the first argument. #2 can be used for the next argument. & is where the arguments are assigned.

intro-to-mathematica_55.gif

intro-to-mathematica_56.png

intro-to-mathematica_57.gif

intro-to-mathematica_58.png

intro-to-mathematica_59.png

intro-to-mathematica_60.png

You can find more on this here.

Import Data

Many times, you'll get data from a csv or xls. Mathematica is pretty good figuring out how to interpret the data.

intro-to-mathematica_61.gif

intro-to-mathematica_62.png

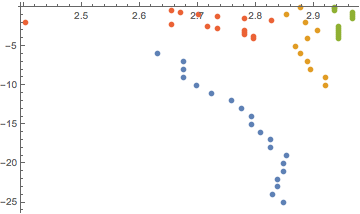
intro-to-mathematica_63.gif

Overlay data

Here, I fit the ε function I defined earlier to the data. I then plot this fit and assign it the name plot1. plot2 is the list plot. By using the Show function, I can overlay these two different plots.

intro-to-mathematica_64.gif

intro-to-mathematica_65.png

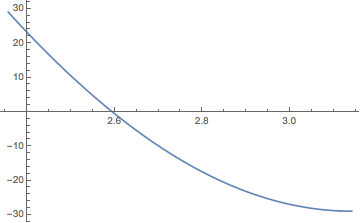
intro-to-mathematica_66.gif

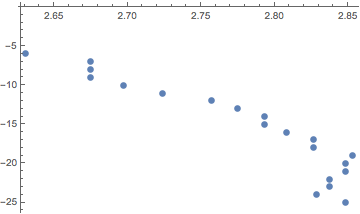
intro-to-mathematica_67.gif

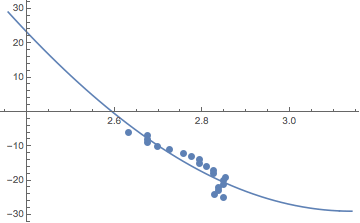
intro-to-mathematica_68.gif

Conclusion

There are a lot of features in Mathematica. It is better to start using Mathematica and gradually learn more features. I recommend using the plot and manipulate functions first. Once you get comfortable with this, you can experiment with more features. You can learn more of the features in the online book “An Elementary Introduction to the Wolfram Language”. Here are some more functions to check out:
Integrate
Derivative
FindPeaks
Polygon
VectorPlot
GraphPlot
Histogram
N
Evaluate
Select
If you want to see some really good examples, check out the demonstrations.

Created with the Wolfram Language